16.3. Insertion sort

What would you do if you have a stack of phone bills from the past two years and you want to order by date? A fairly natural way to handle this is to look at the first two bills and put them in order. Then take the third bill and put it into the right position with respect to the first two, and so on. As you take each bill, you would add it to the sorted pile that you have already made. This simple approach is the inspiration for our first sorting algorithm, called Insertion Sort.

Insertion Sort iterates through a list of records. For each iteration, the current record is inserted in turn at the correct position within a sorted list composed of those records already processed. Given an array named data that stores \(n\) records, one way to implement an insertion sort could be this.

template <class Comparable>
void insertion_sort(Comparable* data[], int n) {
  for (int i = 1; i < n; ++i) {
    for (int j = i; (j > 0) && (*data[j] < *data[j-1]); --j) {
      swap(data, j, j-1);
     }
   }
}

This sort is still \(O(n^{2})\), but works differently from the bubble sort and selection sort, since it always maintains a sorted subvector in the container. Each new item is then “inserted” back into the previous subvector such that the sorted subvector is one item larger. Figure 4 shows the insertion sorting process. The shaded items represent the ordered subvectors as the algorithm makes each pass.

Figure 4: Insertion Sort

We begin by assuming that a vector with one item (position \(0\)) is already sorted. On each pass, one for each item 1 through \(n-1\), the current item is checked against those in the already sorted subvector. As we look back into the already sorted subvector, we shift those items that are greater to the right. When we reach a smaller item or the end of the subvector, the current item can be inserted.

Figure 5 shows the fifth pass in detail. At this point in the algorithm, a sorted subvector of five items consisting of 17, 26, 54, 77, and 93 exists. We want to insert 31 back into the already sorted items. The first comparison against 93 causes 93 to be shifted to the right. 77 and 54 are also shifted. When the item 26 is encountered, the shifting process stops and 31 is placed in the open position. Now we have a sorted subvector of six items.

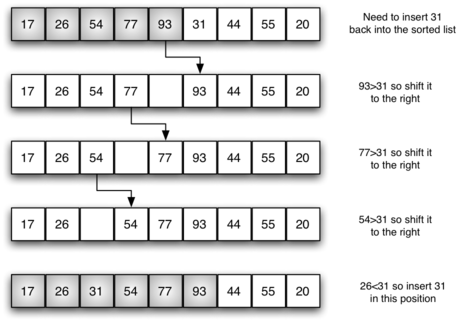
Figure 5: Insertion Sort: Fifth Pass of the Sort

In the following animation, red bars represent the element being looked at and blue represents the last element to look at during a pass.

Initialize Run Stop
Beginning Step Forward Step Backward End

The implementation of insertion_sort (ActiveCode 1) shows that there are again \(n-1\) passes to sort n items. The iteration starts at position 1 and moves through position \(n-1\), as these are the items that need to be inserted back into the sorted subvectors. Line 8 performs the shift operation that moves a value up one position in the vector, making room behind it for the insertion. Remember that this is not a complete exchange as was performed in the previous algorithms.

The maximum number of comparisons for an insertion sort is the sum of the first \(n-1\) integers. Again, this is \(O(n^{2})\). However, in the best case, only one comparison needs to be done on each pass. This would be the case for an already sorted vector.

One note about shifting versus exchanging is also important. In general, a shift operation requires approximately a third of the processing work of an exchange since only one assignment is performed. In benchmark studies, insertion sort will show very good performance.

#include <iostream> #include <vector> using std::vector; vector<int> insertion_sort(vector<int> data) { for (unsigned int index=1; index<data.size(); ++index) { int currentvalue = data[index]; int position = index; while (position>0 && data[position-1]>currentvalue) { data[position] = data[position-1]; --position; } data[position] = currentvalue; } return data; } int main() { vector<int> data = {54, 26, 93, 17, 77, 31, 44, 55, 20}; for (const auto& value: insertion_sort(data)) { std::cout << value << ' '; } std::cout << '\n'; return 0; }

Note

If you have not examined the previous you should. Many job interviews involve a ‘whiteboard interview’ that may ask you to write a bubble sort or an insertion sort.

I don’t know why bubble sort in particular is such a popular question. The bubble sort:

• is not particularly easy to memorize

• is not an obvious solution to the sorting problem

• performs rather badly - it’s average performance is n-squared!

If sorting does get asked and you can get past these points with a future employer, you might score some points with the following examples, which:

• are far easier to memorize and explain: the actual sort is only 2 lines

• even though still n-squared, is typically better in practice than bubble sort

• demonstrates familiarity with the standard library.

#include <algorithm> #include <iostream> #include <iterator> #include <numeric> #include <vector> #include <random> #define RandomAccessIterable typename template <RandomAccessIterable It> void print(const It begin, const It end, const char* msg); template <RandomAccessIterable It> void selection_sort(It begin, It end); template <RandomAccessIterable It> void insertion_sort(It begin, It end); int main() { std::vector<int> v(20); std::iota(v.begin(), v.end(), -10); auto generator = std::mt19937{std::random_device{}()}; std::shuffle(v.begin(), v.end(), generator); print (v.begin(), v.end(), "before: \t"); selection_sort(v.begin(), v.end()); print (v.begin(), v.end(), "selection sort: \t"); std::shuffle(v.begin(), v.end(), generator); print (v.begin(), v.end(), "before: \t"); insertion_sort(v.begin(), v.end()); print (v.begin(), v.end(), "insertion sort: \t"); } template <RandomAccessIterable It> void selection_sort(It begin, It end) { for (auto i = begin; i != end; ++i) { std::iter_swap(i, std::min_element(i, end)); //print (begin, end, "\t"); } } template <RandomAccessIterable It> void insertion_sort(It begin, It end) { for (auto i = begin; i != end; ++i) { std::rotate(std::upper_bound(begin, i, *i), i, std::next(i)); //print (begin, end, "\t"); } } template <RandomAccessIterable It> void print(const It begin, const It end, const char* msg) { // not very pretty // avoids hardcoded ostream_iterator<int> using os = std::ostream_iterator<typename std::iterator_traits<It>::value_type>; std::cout << msg; std::copy(begin, end, os(std::cout, " ")); std::cout << '\n'; }

One nice feature of the selection sort implemented using iter_swap and min_element is that the min_element function takes a custom comparator.

This means that while the default behavior is to sort ascending since the default comparator is std::less any other binary predicate operation could be passed in.

If your compiler supports C++20 ranges, then you could use the ranges versions of min_element and iter_swap and use a range-for loop.

Try This!

Modify the selection_sort template to take an optional comparison function that changes the sort order.

Self Check

sc-1-4: Suppose you have the following list of numbers to sort: [15, 5, 4, 18, 12, 19, 14, 10, 8, 20] which list represents the partially sorted list after three complete passes of insertion sort?

• [4, 5, 12, 15, 14, 10, 8, 18, 19, 20]
• This is the result of bubble sort.
• [15, 5, 4, 10, 12, 8, 14, 18, 19, 20]
• This is the result of selection sort.
• [4, 5, 15, 18, 12, 19, 14, 10, 8, 20]
• Insertion sort works at the start of the list. Each pass produces a longer sorted list.
• [15, 5, 4, 18, 12, 19, 14, 8, 10, 20]
• Insertion sort works on the front of the list not the end.

More to Explore

• Top 5 beautiful C++ algorithms

• Insertion sort

Acknowledgements

This section is adapted from Problem Solving with Algorithms and Data Structures using C++, by Brad Miller and David Ranum, Luther College, and Jan Pearce, Berea College released under the CC BY-NC-SA 4.0, and Open Data Structures (OpenDSA) by Ville Karavirta and Cliff Shaffer which is distributed under the MIT License.

You have attempted of activities on this page