6.3. Example: Converting an Integer to a String¶
Suppose you want to convert an integer to a string in some base between
binary and hexadecimal. For example, convert the integer 10 to its
string representation in decimal as "10", or to its string
representation in binary as "1010". While there are many algorithms
to solve this problem, the recursive formulation of the problem is
elegant.
Let’s look at a concrete example using base 10 and the number 769.
Suppose we have a sequence of characters corresponding to the first 10
digits, like digits = "0123456789". It is easy to convert a
number less than 10 to its string equivalent by looking it up in the
sequence. For example, if the number is 9, then the string is
digits[9] or "9". If we can arrange to break up the number
769 into three single-digit numbers, 7, 6, and 9, then converting it to
a string is simple. A number less than 10 sounds like a good base case.
Knowing what our base is suggests that the overall algorithm will involve three components:
Reduce the original number to a series of single-digit numbers.
Convert the single digit-number to a string using a lookup.
Concatenate the single-digit strings together to form the final result.
The next step is to figure out how to change state and make progress toward the base case. Since we are working with an integer, let’s consider what mathematical operations might reduce a number. The most likely candidates are division and subtraction. While subtraction might work, it is unclear what we should subtract from what. Integer division with remainders gives us a clear direction. Let’s look at what happens if we divide a number by the base we are trying to convert to.
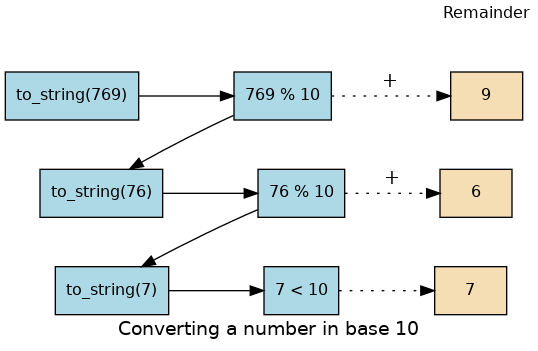
Using integer division to divide 769 by 10, we get 76 with a remainder of 9. This gives us two good results. First, the remainder is a number less than our base that can be converted to a string immediately by lookup. Second, we get a number that is smaller than our original and moves us toward the base case of having a single number less than our base. Now our job is to convert 76 to its string representation. Again we will use integer division plus remainder to get results of 7 and 6 respectively. Finally, we have reduced the problem to converting 7, which we can do easily since it satisfies the base case condition of \(n < base\), where \(base = 10\). The series of operations we have just performed is illustrated in the figure below. Notice that the numbers we want to remember are in the remainder boxes along the right side of the diagram.
1std::string to_string(int n, int base) {
2 const char* digits = "0123456789ABCDEF";
3 if (n < base) {
4 return std::string(1, digits[n]);
5 }
6 return to_string(n/base, base).append(1, digits[n%base]);
7}
Notice that in line 3 we check for the base case where n
is less than the base we are converting to.
When we detect the base case,
recursion stops and a char from digits is returned.
The final return on line 6 satisfies both the second and third properties of recursion - by making the recursive call and by reducing the problem size using division.
Note
The standard library includes a set of functions called std::to_string to convert a variety of numeric types into a std::string, but it does not handle arbitrary change of base.
Let’s trace the algorithm again; this time we will convert the number 10
to its base 2 string representation ("1010").
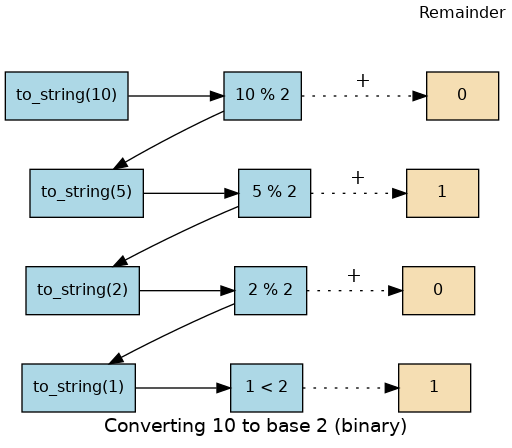
The previous figure shows that we get the results we are looking for,
but it looks like the digits are in the wrong order. The algorithm works
correctly because we make the recursive call first on line
6, then we add the string representation of the remainder.
If we reversed returning the digits lookup and returning the
to_string call, the resulting string would be backward! But by delaying
the concatenation operation until after the recursive call has returned,
we get the result in the proper order.
More to Explore
Content on this page is adapted from Problem Solving with Algorithms and Data Structures using C++, section 4.5. Copyright (C) Brad Miller, David Ranum. under the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/.