6.4. The Binary Tree ADT

Unlike the linear sequences covered so far, a tree is a hierarchical abstract data type. Conceptually, it can be thought of as a collection of nodes defined by parent-child relationships.

Refer to Tree ADT concepts to review the basic vocabulary and structure of binary trees.

So far, we have discussed trees only at a conceptual level. In this section we will program one.

In a binary tree, one node is the root. It serves as the ‘trunk’ of the tree and serves the same function as the head of a list The root node is the only node in a tree without a parent. All other nodes in a tree refer to exactly 1 parent. In a binary tree, the children are commonly referred to as the left and right children.

A simple binary tree can be implemented as a recursive data structure:

template <class T>
 struct tree {
    T value;
    tree<T>* left = nullptr;
    tree<T>* right = nullptr;
};

This tree stores a single value of type T and has two pointers to potential children. It is important to remember when working with a recursive tree such as this that a child might be a nullptr.

6.4.1. Binary tree traversal

Traversal of a data structure means visit elements of the structure. It might mean visiting a subset, but can also involve visiting each element from the first to last.

For sequential containers, identifying the start and end of the container is simple. But where are the first and last elements of a tree?

The short answer is that there is no single answer. Since a tree is not a sequential data structure, a tree allows for different sequences (or traversals). There are several different types of traversals. The most common tree traversals are:

• Preorder

• Postorder

• Inorder

• Level order

Given the following binary tree, let’s implement functions that traverse the tree using each of the four methods.

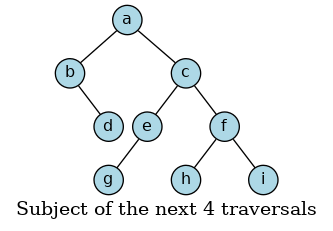
6.4.1.1. Preorder traversal

A depth first traversal.

Visit all nodes before visiting children:

In this generic code block, the function visit represents the action to take on the current node.

void preorder(tree<T>* node) {
  if (node == nullptr) {
    return;
  }
  visit(node);
  preorder(node->left);
  preorder(node->right);
}

#include <iostream> template <class T> struct tree { T value; tree<T>* left = nullptr; tree<T>* right = nullptr; }; template <class T> void print(tree<T>* node) { if (node == nullptr) { return; } std::cout << node->value << ' '; print(node->left); print(node->right); } ==== int main() { tree<char> a; tree<char> b; tree<char> c; tree<char> d; tree<char> e; tree<char> f; tree<char> g; tree<char> h; tree<char> i; a.value = 'a'; b.value = 'b'; c.value = 'c'; d.value = 'd'; e.value = 'e'; f.value = 'f'; g.value = 'g'; h.value = 'h'; i.value = 'i'; a.left = &b; a.right = &c; b.right = &d; c.left = &e; c.right = &f; e.left = &g; f.left = &h; f.right = &i; std::cout << "Preorder: "; print (&a); return 0; }

6.4.1.2. Postorder traversal

A depth first traversal.

Visit all nodes after visiting children:

void postorder(tree<T>* node) {
  if (node == nullptr) {
    return;
  }
  postorder(node->left);
  postorder(node->right);
  visit(node);
}

The only difference between the preorder example and this is the order of the function calls in the print function.

#include <iostream> template <class T> struct tree { T value; tree<T>* left = nullptr; tree<T>* right = nullptr; }; template <class T> void print(tree<T>* node) { if (node == nullptr) { return; } print(node->left); print(node->right); std::cout << node->value << ' '; } ==== int main() { tree<char> a; tree<char> b; tree<char> c; tree<char> d; tree<char> e; tree<char> f; tree<char> g; tree<char> h; tree<char> i; a.value = 'a'; b.value = 'b'; c.value = 'c'; d.value = 'd'; e.value = 'e'; f.value = 'f'; g.value = 'g'; h.value = 'h'; i.value = 'i'; a.left = &b; a.right = &c; b.right = &d; c.left = &e; c.right = &f; e.left = &g; f.left = &h; f.right = &i; std::cout << "Postorder: "; print (&a); return 0; }

6.4.1.3. Inorder traversal

A depth first traversal.

Visit the left child (and the left child subtree), then visit the current node, then visit the right child (and the right child subtree),

void inorder(tree<T>* node) {
  if (node == nullptr) {
    return;
  }
  inorder(node->left);
  visit(node);
  inorder(node->right);
}

#include <iostream> template <class T> struct tree { T value; tree<T>* left = nullptr; tree<T>* right = nullptr; }; template <class T> void print(tree<T>* node) { if (node == nullptr) { return; } print(node->left); std::cout << node->value << ' '; print(node->right); } ==== int main() { tree<char> a; tree<char> b; tree<char> c; tree<char> d; tree<char> e; tree<char> f; tree<char> g; tree<char> h; tree<char> i; a.value = 'a'; b.value = 'b'; c.value = 'c'; d.value = 'd'; e.value = 'e'; f.value = 'f'; g.value = 'g'; h.value = 'h'; i.value = 'i'; a.left = &b; a.right = &c; b.right = &d; c.left = &e; c.right = &f; e.left = &g; f.left = &h; f.right = &i; std::cout << "Inorder: "; print (&a); return 0; }

6.4.1.4. Level order traversal

Differs from the previous traversals: it is a ‘breadth first’ traversal. Also, this algorithm is easier to implement iteratively than recursively.

Visit each node on each level of the tree then visit the children one level deeper.

This is an iterative, not a recursive function.

void levelorder(tree<T>* node) {
  if (node == nullptr) {
    return;
  }
  std::queue<tree<T>*> q;
  q.push(node);
  while (!q.empty()) {
    auto tmp = q.front();
    visit(tmp);
    q.pop();
    if(tmp->left)  q.push(tmp->left);
    if(tmp->right) q.push(tmp->right);
  }
}

#include <iostream> #include <queue> template <class T> struct tree { T value; tree<T>* left = nullptr; tree<T>* right = nullptr; }; template <class T> void print(tree<T>* node) { if (!node) return; std::queue<tree<char>*> q; q.push(node); while (!q.empty()) { auto tmp = q.front(); std::cout << tmp->value << ' '; q.pop(); if(tmp->left) q.push(tmp->left); if(tmp->right) q.push(tmp->right); } } ==== int main() { tree<char> a; tree<char> b; tree<char> c; tree<char> d; tree<char> e; tree<char> f; tree<char> g; tree<char> h; tree<char> i; a.value = 'a'; b.value = 'b'; c.value = 'c'; d.value = 'd'; e.value = 'e'; f.value = 'f'; g.value = 'g'; h.value = 'h'; i.value = 'i'; a.left = &b; a.right = &c; b.right = &d; c.left = &e; c.right = &f; e.left = &g; f.left = &h; f.right = &i; std::cout << "Level order: "; print (&a); return 0; }

---

More to Explore

• STL containers library

• Visualgo: binary heap

You have attempted of activities on this page