12.3. The queue class

A queue is another special purpose container adapter that limits random element access to all parts of the storage. A queue is just another word for a line. Like a stack, a queue restricts element access to the ends. Unlike a stack, a queue allows access to both ends:

Imagine a line at the bank or a store. An orderly queue means that the people who get in line first are the first customers called. This is the guarantee queue enforces. A queue is a FIFO (first-in, first-out) data structure.

The std::queue is a container adapter that gives the programmer the functionality of a queue.

The class template acts as a wrapper to the underlying container - only a specific set of functions is provided. The queue pushes elements on the back of the underlying container, and pops them from the front.

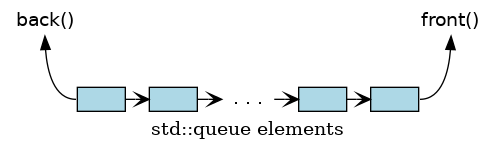
std::queue elements

The defining operations of a queue are:

push

Add a new element to the back (end) of the queue.

pop

Remove an element from the front (beginning) of the queue.

front

Get the value of the element at the beginning of the queue.

back

Get the value of the element at the end of the queue.

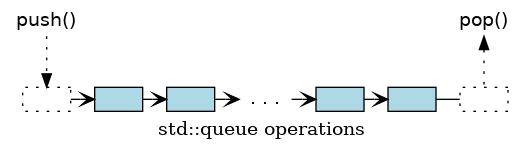
std::queue operations

Minor modifications change pop_all() from a function performing stack operations into one performing queue operations:

#include <iostream>
#include <queue>

#define QueueContainer typename

template <QueueContainer C>
void pop_all(C& q) {
  while(!q.empty()) {
    std::cout << q.front() << " ";
    q.pop();
  }
  std::cout << "\npopped all from queue\n";
}

The STL containers std::list and std::deque can be adapted to create a queue.

12.3.1. Circular queues

A circular queue, cyclic buffer, or ring buffer is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end. A ring buffer is a good choice when you need the behavior of a queue and the buffer size can be fixed.

There are many ways to implement this data structure and the following is just an example of one.

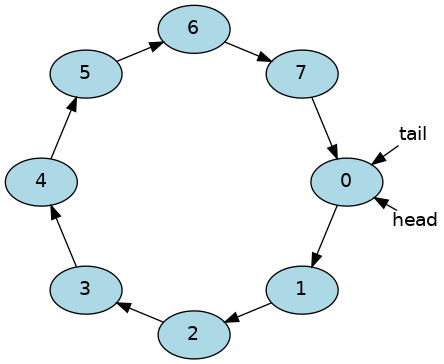
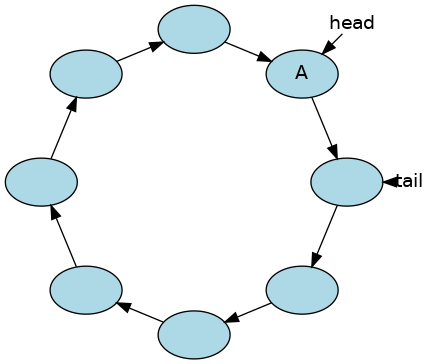
Conceptually, a circular buffer is a closed ring of data.

  • One element needs to be chosen as the start of the data. The terms start, begin, or head are all reasonable.

  • One element needs to be chosen as the end of the data. The terms last, end, or tail are all reasonable.

The start locations of head and tail are arbitrary.

A ring buffer is initially empty and of some predefined length. For example, this is an 8-element buffer conceptually:

empty buffer

The tail node always refers to the element just past the end of our data (as always). So when the head and tail are equal, the buffer is empty.

The capacity is the maximum number of elements that can be stored in the buffer. In this example, the capcacity is 8.

The size is the current number of elements used in the buffer. In our initially empty buffer, the size is 0.

Since there are no true circular sections of memory, it is normal to represent a circular buffer in a normal contiguous linear memory block. An array is a good choice.

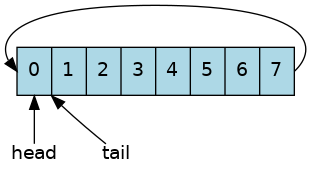
empty buffer - linear representation

Adding one element to the buffer involves storing a new value at the tail location and moving the tail.

add one to buffer

And in the array:

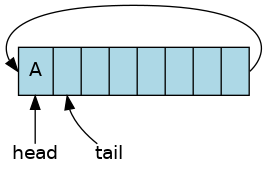
add one - linear representation

The buffer size is now 1.

If two more items are added, the tail moves accordingly. The head does not move as items are added.

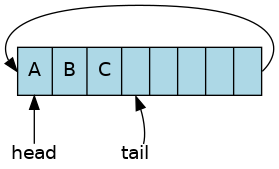
add two more to buffer

The buffer size is now 3.

Removing an element from the buffer involves

  • returning the oldest element from the buffer

  • moving the head

  • decrease buffer size

As with earlier containers, there is no need to erase the oldest element, since after the head has moved, we can no longer access it.

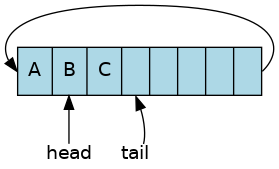
remove 1 element

The buffer size is now 2.

Starting with our buffer containing [B,C], we can add elements until it is completely full.

Recall we popped A from this buffer earlier.

Adding a few elements moves the tail and increases the size.

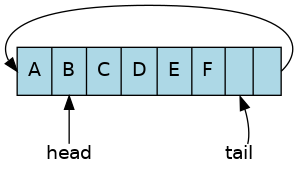
adding more to buffer

At this point the buffer is almost full. The tail now refers to the first element in the array. It needed to wrap around to avoid potentially allowing a write outside the array bounds. The slot containing ‘A’ is available for writing, since it was removed earlier.

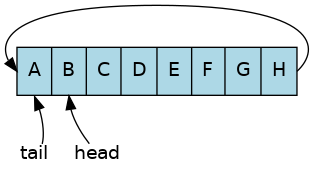
almost full buffer

One more write to the element at position 0 and now the buffer is completely full.

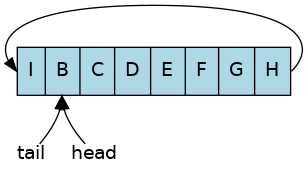
full buffer

The buffer size is now 8. It is important to note that in this implementation head == tail does not represent the idea of an empty buffer. In this implementation the head == tail state can mean either a completely empty or a full queue.

An extra variable size is used to distinguish empty from full, since we know the array size ahead of time. If we chose to not keep track of size and use only the head and tail then the maximum size of the would be \(capacity - 1\).

Different designs could result in different outcomes, there are no hard and fast rules here. I chose this implementation because it is easy to reason about and does not waste a storage slot, at the cost of an additional variable.

What do we do when our buffer is full? At this point, we have choices:

  • Allow no writes to the buffer until elements are removed.

    This is common when it is important to never lose any information, such as when processing keystrokes from the user, or managing a print queue.

  • Allow writes to overwrite the oldest elements. The oldest values are lost in favor of new values.

    This implementation is used when the oldest information may no longer be important enough by the time the buffer is full.

More to Explore

You have attempted of activities on this page