12.2. The stack class

Sometimes we want to limit access to all parts of a sequential data structure. In other words, we want to store as much data as we want to, but we want to restrict the ability to access any element at random. One way to limit access to only one end of a container is to use a stack.

Imagine creating a pile by adding items one at a time on top of each other:

• plates

• pancakes

• sheets of paper

• stones

Any of these visual analogies you prefer will work. Each of them is a stack. In each case, adding items to the top of the stack makes other items deeper in the stack inaccessible. The only way to observe or remove an item from the stack is to remove all of the items above it first.

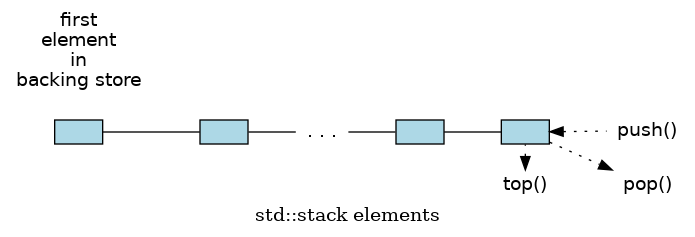
Because the first item added to a stack is also the item farthest from the top of the stack, we refer to a stack as a Last-In-First-Out (LIFO) data structure.

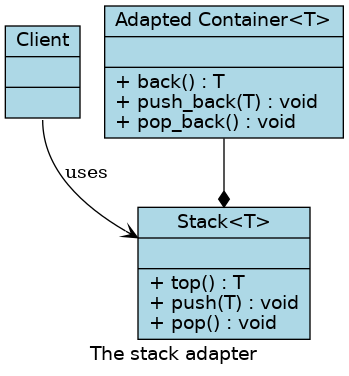
The std::stack is a container adapter that gives the programmer the functionality of a stack.

The class template acts as a wrapper to the underlying container - only a specific set of functions is provided. The stack pushes and pops the element from the back of the underlying container, known as the top of the stack.

Given a std::stack<T>, the defining operations of a stack are:

void push (T value)

Add a new element to the top of the stack.

void pop()

Remove an element from the top of the stack.

T top()

Get the value of the element at the top of the stack.

Before running the following example, predict the output, then check yourself.

#include <iostream> #include <stack> #include <string> using std::cout; using std::stack; // remove all elements from a stack and print them out template <class Container> void pop_all(Container& s) { while(!s.empty()) { cout << s.top() << " "; s.pop(); } cout << "\npopped all from stack\n"; } int main () { stack<std::string> strings; cout << "push strings onto stack...\n"; strings.push("one"); strings.push("two"); strings.push("three"); strings.push("four"); strings.push("five"); cout << "size of stack before: " << strings.size() << '\n'; pop_all (strings); cout << "size of stack after: " << strings.size() << '\n'; if (strings.empty()) { cout << "stack is empty.\n"; } return 0; }

It is also possible to initialize a stack from another container. The initializing container must match the container adapted for the stack instance. By default, deque is used, but any container that provides

• back()

• push_back()

• pop_back()

can be used as a stack adapter. In the STL, besides deque, vector and list also can be adapted by a stack.

Because the default backing store for a stack is a deque, a container adapter does not need to be specified.

// initialize stack from deque
std::deque<int> x = { 1, 2, 3, 4, 5 };
stack<int>> numbers(x);

To copy a list into a stack will only work if the stack instance uses a list as its backing store.

// initialize stack from list
std::list<int> y = { 1, 2, 3, 4, 5 };
stack<int, std::list<int>> numbers(y);

Before running the following example, predict the output, then check yourself.

#include <iostream> #include <stack> #include <list> using std::cout; using std::stack; // remove all elements from a stack and print them out template <class Container> void pop_all(Container& s) { while(!s.empty()) { cout << s.top() << " "; s.pop(); } cout << "\npopped all from stack\n"; } int main () { cout << "initialize stack from list:\n"; std::list<int> tmp = { 1, 2, 3, 4, 5 }; stack<int, std::list<int>> numbers(tmp); cout << "list has " << tmp.size() << " entries\n"; pop_all (numbers); if (numbers.empty()) { cout << "stack is empty.\n"; } return 0; }

Notice the elements from the list are pushed onto the stack in the order they are retrieved from the list. The number 1 is pushed first, so when initialization is complete, it is on the bottom of the stack.

Stack elements cannot be accessed directly in the way you are used to with other sequential containers like arrays, vectors, and lists. To ‘visit’ each element in a stack, the items need to be popped off.

If you think you need to visit all the elements in a stack, then you probably should not be using a stack.

12.2.1. Postfix Notation

A compiler generates machine instructions required to carry out the statements of a source program written in a high-level language. One part of this task is to generate instructions for evaluating arithmetic expressions such as

value = a * (b + c);

In most programming languages, arithmetic expressions are written using infix notation as in the above example. The symbol for each binary operation is placed between the operands. Many compilers first transform infix expressions into postfix notation, and then generates machine instructions to evaluate these postfix expressions. This two-step process is used because transformations from infix to postfix is straightforward, and postfix expressions are generally easier to evaluate than infix expressions.

In postfix notation the operator follows the operands and parentheses are not needed. In the earlier example, the infix expression:

2 * (3 + 5);

can be re-written as a postfix expression:

2 3 5 + *

Evaluation this expression proceeds left to right:

// Scan numbers until the first operator is encountered
// operate on the operands immediately to the left
// of the operator
2 3 5 + *

// becomes
2 8 *

// which becomes
16

This method of evaluating a postfix expression requires that the operands be stored until an operator is encountered in the left-to-right scan. Once an operator is found, the last two operands must be retrieved and combined using the operation encountered. This suggests that a stack should be used to store the operands.

Each time an operand is encountered, it is pushed onto the stack. Then, when an operator is encountered, the top two values are popped from the stack; the operation is applied to them, and the result is pushed back onto the stack.

---

More to Explore

• STL containers library

• STL stack class

• MyCodeSchool video: Data structures: introduction to stack

You have attempted of activities on this page