2.7. Analysis of Vector Operators¶

Accessing data using an index and assigning to an index position that already exists both take the same amount of time no matter how large the vector is. When an operation like this is independent of the size then it is \(O(1)\).

As we have seen, one way to create a longer vector is to use the push_back() method. The push_back() method is typically \(O(1)\), provided there is adequate capacity in the underlying array.

First we’ll use push_back() method. The following code shows the code for making our vector.

#include <vector>
using std::vector;

void test_push_back(int size){
    vector<int> vect;
    for (int i = 0; i < size; ++i){
        vect.push_back(i);
    }
}

And we can time how long it takes to push 10,000 values into a vector.

In the experiment above the statement that we are timing is the function call to test_push_back. From the experiment, we see the amount of time taken by the push_back operation. Not only is the push_back() function call duration being measured, but the time to allocate space is being measured.

We can improve the runtime a bit further by setting an adequate reserve for the vector in advance. Doing this will keep us from having to move the entire vector to an adequately sized space in memory as the vector grows.

#include <chrono>
#include <iostream>
#include <iomanip>
#include <vector>
using std::vector;

void test_push_back(int size){
    vector<int> vect;
    for (int i = 0; i < size; ++i){
        vect.push_back(i);
    }
}

void test_reserve(int size){
    vector<int> v(size);
    for (int i = 0; i < size; ++i){
        v[i] = i;
    }
}

int main(){
    using std::cout;
    using std::chrono::steady_clock;
    using msec_t = std::chrono::duration<double, std::milli>;

cout << std::setw(6) << "size\t"
         << std::setw(8) << "push_back\t"
         << std::setw(8) << "pre-allocated vector (all times in msec)\n";

for(int size = 1'000; size < 1'000'000; size += 50'000) {

auto begin = steady_clock::now();
      test_push_back(size);
      auto end = steady_clock::now();
      msec_t elapsed_1 = end - begin;

auto begin2 = steady_clock::now();
      test_reserve(size);
      auto end2 = steady_clock::now();
      msec_t elapsed_2 = end2 - begin2;

cout << std::setprecision(6) << std::fixed
           << size << '\t'
           << std::setw(8) << elapsed_1.count() << '\t'
           << std::setw(8) << elapsed_2.count() << '\n';
    }
    return 0;
}

A graph of the loops in the preceding code should look something like this:

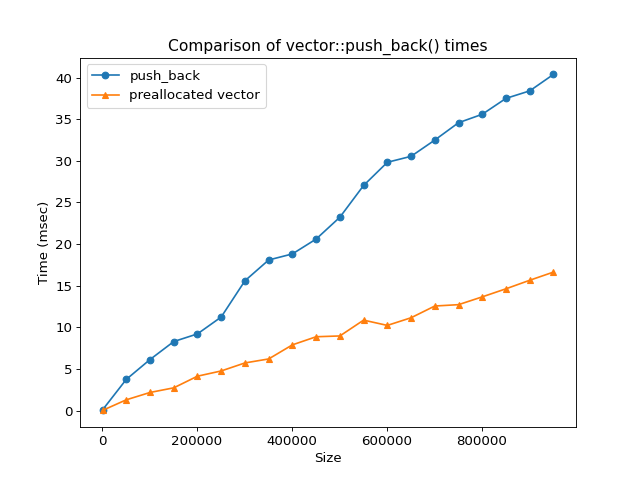
Now that we have seen how performance can be measured concretely you can look at the table below to see the Big-O efficiency of some basic vector operations. When pop_back() is called, the vector size is reduced by 1 and it takes constant time: \(O(1)\). However, when erase() is called the time is \(O(n)\). The reason for this lies in how C++ chooses to implement vectors. When an item is taken from the front of the vector, in C++ implementation, all the other elements in the vector are shifted one position closer to the beginning. This implementation also allows the index operation to be \(O(1)\). This is a trade-off that the C++ implementers thought was a good one.

**Big-O Efficiency of C++ Vector Operators**¶
Operation	Big-O Efficiency
index []	O(1)
index assignment =	O(1)
push_back()	amortized O(1)
pop_back()	O(1)
erase(i)	O(n)
insert(i, item)	O(n)
find(b, e, item)	O(n)
reserve()	O(n)
begin()	O(1)
end()	O(1)
size()	O(1)

The push_back() operation is \(O(1)\) unless there is inadequate capacity, in which case the entire vector is moved to a larger contiguous underlying array, which is \(O(n)\). However, since over the long term, as \(n\) grows large, then number of vector copies is small. So on average, even though there are some \(O(n)\) operations, it turns out that push_back() is constant time.

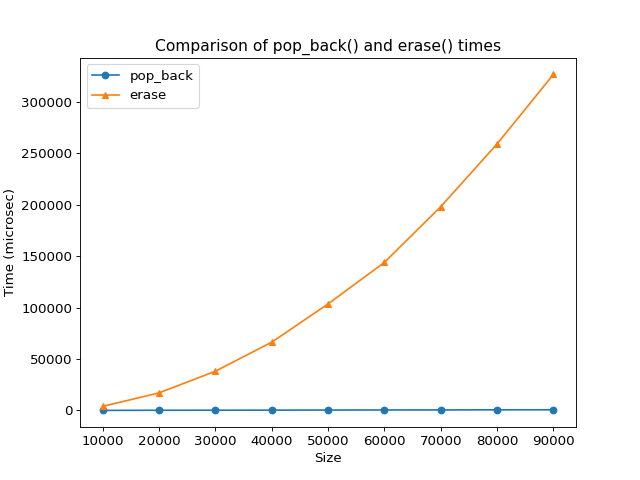
As a way of demonstrating the difference in performance between pop_back() and erase(), let’s do another timing experiment. Our goal is to be able to verify the performance of the pop_back() operation on a vector of a known size when the program pops from the end of the vector using pop_back(), and again when the program pops from the beginning of the vector using erase(). We will also want to measure this time for vectors of different sizes. What we would expect to see is that the time required to pop from the end of the vector will stay constant even as the vector grows in size, while the time to pop from the beginning of the vector will continue to increase as the vector grows.

The following code shows one way to measure the difference between the pop_back() and erase().

#include <chrono>
#include <iostream>
#include <iomanip>
#include <numeric>
#include <vector>
using std::vector;

int main(){
    using std::cout;
    using std::chrono::steady_clock;
    using msec_t = std::chrono::duration<double, std::micro>;

cout << std::setw(6) << "size\t"
         << std::setw(8) << "pop_back\t"
         << std::setw(8) << "erase\t\t"
         << std::setw(8) << "how much faster is pop_back?\n";
    cout << std::setw(19) << "(microsec)\t"
         << std::setw(10) << "(microsec)\n";

for(int size = 10'000; size < 100'000; size += 10'000) {
        // Create 2 identical vectors with values 0..N
        vector<int> data1(size);
        std::iota(data1.begin(), data1.end(), 0);
        vector<int> data2(data1);

auto begin1 = steady_clock::now();
      for (int i = 0; i < size; i++){
        data1.pop_back();
      }
      auto end1 = steady_clock::now();
      msec_t elapsed_1 = end1 - begin1;

auto begin2 = steady_clock::now();
      for (int i = 0; i < size; i++){
        data2.erase(data2.begin());
      }
      auto end2 = steady_clock::now();
      msec_t elapsed_2 = end2 - begin2;

cout << std::setprecision(6) << std::fixed
           << size << '\t'
           << std::setw(8) << elapsed_1.count() << '\t'
           << std::setw(8) << elapsed_2.count() << "\t"
           << std::setprecision(0)
           << std::setw(8) << elapsed_2.count() / elapsed_1.count() << " times\n";
    }
    return 0;
}

Although erase is \(O(n)\), a graph showing how much faster pop_back() can be as the size of a vector grows can still be surprising.

Self Check

sc-1-4: Drag the operation(s) on the left to their corresponding Big(O)

Review operations and thier Big(O)

begin(), end(), size(), index [], index assignment = ,push_back(), pop_back()
O(1)
reserve(), erase(i), insert(i, item),find(srt, stp, item)
O(n)
find(srt, stp, item)
O(log n)

More to Explore

You have attempted of activities on this page