14.3. Binary Search Tree iterators

The recursive traversal algorithms work well for implementing tree-based ADT member functions, but if we are trying to hide the trees inside some ADT for example, using binary search trees to implement std::set or using STL algorithms or range-for loops, then we need to provide iterators for walking though the contents of the tree.

Iterators for tree-based data structures can be more complicated than those for linear structures.

For arrays (and vectors and deques and other array-like structures) and linked lists, a single pointer can implement an iterator.

Given the current position, it is easy to move forward to the next element.

For anything but a singly-linked list, we can also easily move backwards.

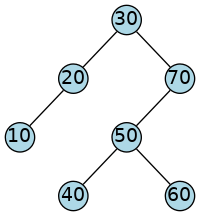
a binary search tree

But look at this binary search tree, and suppose that you were implementing tree iterators as a single pointer. Let’s see if we can “think” our way through the process of traversing this tree one step at a time, without needing to keep a whole stack of unfinished recursive calls around.

We’re going to try to visit the nodes in the same order we would process them during an “in-order” traversal. For a BST, in-order traversal means that we will visit the data in ascending order.

It’s not immediately obvious what our data structure for storing the “current position” (i.e., an iterator) will be. We might suspect that a pointer to a tree node will be part of that data structure, because that worked with iterators over linked lists.

14.3.1. BST iterator begin() and end()

As in any data structure, begin and end refer to the first element in the data structure and one past the last element. In the last section, we said that a BST is sorted when a level order traversal is used.

So what algorithm should we use to find the beginning?

So what algorithm should we use to find the end?

14.3.2. BST iterator operator++()

A quick review of the definition of iterators and the iterator design pattern. We have a few facts to deal with:

  • A tree is a hierarchical data structure

  • An iterator allows users to visit each element in a container sequentially - with no awareness of the underlying structure.

  • In C++, iterators are implemented using pointer semantics. The function operator++() is used to move to the next element.

Given our familiar tree:

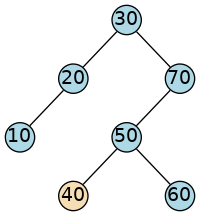
a binary search tree

If we are iterating through our tree and are currently at the node with value 40, then how do we get to the next node?

In a binary tree, to get to the next node, we need to know not only where we are, but also how we got here.

One way is to do that is to implement the iterator as a stack of pointers containing the path to the current node. The stack would be used to simulate the activation stack during a recursive traversal.

But this solution is clumsy and inefficient. Iterators tend to get assigned (copied) a lot, and we’d really like that to be a constant time - an O(1) operation. Having to copy an entire stack of pointers just isn’t very attractive.

14.3.2.1. BST iterator using parent pointers

We can make the task of creating tree iterators much easier if we redesign the tree nodes to add pointers from each node to its parent.

// a binary tree node
template<class T>
  struct tree_node {
    T value;
    tree_node<T>* left;
    tree_node<T>* right;
    tree_node<T>* parent; // link to parent simplifies iterators
    tree_node(const T& value = T{},
        tree_node<T>* left = nullptr,
        tree_node<T>* right = nullptr,
        tree_node<T>* parent = nullptr)
      : value{value}
    , left{left}
    , right{right}
    , parent{parent}
    { }
  };

These nodes are then used to implement a tree class, which, as usual, keeps track of the root of our tree in a data member.

The outline for a tree iterator is similar to what we have covered before:

template <typename T>
  struct tree_iterator {
    typedef T value_type;
    typedef T* pointer;
    typedef T& reference;
    typedef std::ptrdiff_t difference_type;
    typedef std::bidirectional_iterator_tag iterator_category;

    const tree::tree_node<T>* node;
    tree_iterator() = default;
    tree_iterator(const tree::tree_node<T>* n);

    constexpr
       const T& operator*() const noexcept;
    tree_iterator& operator++();
    tree_iterator operator++(int);
    tree_iterator& operator--();
    tree_iterator operator--(int);
 };

There is a subtlety when using our tree iterator in a BST.

template<class T>
 class bstree {
   public:
     typedef T value_type;
     typedef const tree_iterator<T> const_iterator;
     typedef const_iterator iterator;
     typedef const_iterator reverse_iterator;
     typedef const_iterator const_reverse_iterator;

     // remainder omitted . . .
 };

Note the type of all the iterators is const. We only want const behavior for this ADT. If we provided a “true” non-const iterator, it would allow reassigning data in the tree:

bstree<int>::iterator it = myTree.find(50);
*it = 10000;

which would very likely break the internal ordering of data, violating the binary search tree property, and making it useless for any future searches. A const iterator allows us to look at data in the container, but not change that data.

14.3.3. Implementing BST iterators

As discussed earlier, begin() is implemented by finding the minimum element in the tree.

A free function that works with the tree_node struct is enough:

template <class T>
  tree_node<T>* min_element(tree_node<T>* root )
  {
    if(root == nullptr || root->left == nullptr) {
      return root;
    }
    return min_element(root->left);
  }

bstree::begin() can use this function directly:

constexpr
  const_iterator begin() const noexcept {
    return const_iterator(min_element(root));
  }

And end() uses the null pointer.

constexpr
  const_iterator end() const noexcept {
    return const_iterator(nullptr);
  }

14.3.3.1. Implementing operator++()

Before implementing operator++, let’s think about what is should do. Given the following tree:

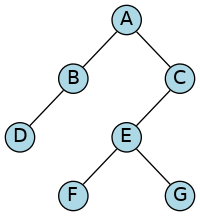
a binary tree of letters

(Not a binary search tree, just a tree).

Question: Suppose that we are currently at node E. What is the in-order successor of E? That is, the node that comes next during an in-order traversal of E?

That example suggests that a node’s in-order successor tends to be among its right descendants.

If our previous premise is correct, then what is the in-order successor to A?

This suggests that, if a node has any right descendants, we should:

  • Take a step down to the right, then

  • Run as far down to the left as we can.

You can see how this would take us from A to F. The same approach would take us from E to G as well. So both of our prior examples are satisfied.

But that “step to the right, then run left” procedure raises a new question. What happens if we are at a node with no right descendants?

Question: Suppose that we are currently at node C. What is the in-order successor of C?

While node C is an interesting special case, it doesn’t make clear what should happen in the more general case where we have no right child.

Question: What is the in-order successor of F?

Question: What is the in-order successor of G?

Why did we move up two steps in the tree this time, when from F we only moved up one step? The answer lies in whether we moved back up over a left-child edge or a right-child edge.

If we move up over a right-child edge, we’re returning to a node that has already had all of its descendants, left and right, visited. So we must have already visited this node as well, otherwise we would never have made it into its right descendants.

If we move up over a left-child edge, then we’re returning to a node that has already had all of its left descendants visited but none of its right descendants. That’s the definition of when we want to visit a node during an in-order traversal, so it’s time to visit this node.

So, if a node has no right child, we move up in the tree (following the parent pointers) until we move back over a left edge. Then we stop.

When applying this procedure to C, we move up to A (right edge), then try to move up again to A’s parent. But since A is the tree root, it’s parent pointer will be null, which is our signal that C has no in-order successor.

To summarize:

  • If the current node has a non-null right child,

    • Take a step down to the right

    • Then run down to the left as far as possible

  • If the current node has a null right child,

    • Move up the tree until we have moved over a left child link

Putting it all together.

tree_iterator& operator++() {
  if (node == nullptr) {
    return * this;
  }
  if (node->right != nullptr) {
     // find the smallest node on the right subtree
     node = mesa::tree::min_element(node->right);
  } else {
     // finished with right subtree and there is no right
     // search up for first parent with a non-null right child
     // or nullptr,
     auto parent = node->parent;
     while (parent != nullptr && node == parent->right) {
       node = parent;
       parent = parent->parent;
     }
     node = parent;
  }
  return * this;
}

One part of this iterator that needs closer inspection is the while loop. This loop continues moving upwards in the tree until it finds:

  • A node where the current node is in the left subtree of its parent, or

  • The root of the tree (parent == nullptr), indicating that there is no in-order successor (end of the traversal).

Key Conditions

  • parent != nullptr: Ensures we do not dereference a nullptr when accessing parent->right.

  • node == parent->right: Asserts the current node is the right child of its parent. When true, we need to keep moving upwards, as the in-order successor is not in this part of the tree.

The loop climbs up the tree until it finds a node for which the current traversal has completed its right subtree. This ensures that the in-order successor is correctly identified.

Consider an alternative approach that simply checks the immediate predecessor:

if (parent != nullptr && node == parent->right) {
    node = parent;
    parent = parent->parent;
}

The issue with this approach is that it would only handle one level of traversal upwards. If the current node is deeply nested in a right subtree, it may skip multiple ancestors that need to be visited to find the in-order successor. This can cause incorrect results when:

  • The node is the rightmost descendant of a deep subtree, requiring multiple upward traversals to reach the root or an ancestor in a left subtree.

  • Randomly generated trees or trees that have had many insertions and removals from the tree may have imbalanced structures with chains of right children, requiring multiple iterations of the while loop.

Consider this tree:

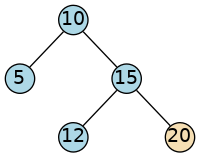
a binary search tree

If the iterator is at 20 (the rightmost node):

  • The while loop will correctly climb from 20 –> 15 –> 10, and stop when parent == nullptr.

  • A single conditional would move only one step (to 15) and fail to reach the root, leaving the iterator in an inconsistent state.

14.4. Using parent pointers

Using parent pointers does incur additional overhead. We must store an additional pointer with every tree node. It also means the functions used to manage the tree need to change.

Originally, inserting a node looked like this:

tree::tree_node<T>*
 insert (const T& value,
         tree::tree_node<T>*& node)
 {
   // add a new leaf
   if(node == nullptr) {
     node = new tree::tree_node<T>(value, nullptr, nullptr);
     return node;
   }
   if(value < node->value) {
     return insert(value, node->left);
   }
   if(node->value < value) {
     return insert(value, node->right);
   }
   // else the value already exists in the tree
   node->value = value;
   return node;
 }

But now when inserting a new node, we also need to maintain correct parent relationships.

tree::tree_node<T>*
  insert (const T& value,
          tree::tree_node<T>*& node,
          tree::tree_node<T>* parent)
  {
    // add a new leaf
    if(node == nullptr) {
      node = new tree::tree_node<T>(value, nullptr, nullptr, parent);
      return node;
    }
    if(value < node->value) {
      return insert(value, node->left, node);
    }
    if(node->value < value) {
      return insert(value, node->right, node);
    }
    // else the value already exists in the tree
    node->value = value;
    return node;
  }

When we make a new node, we need to pass the parent into the tree_node constructor. Even though it won’t have children initially, it will have a parent.

When we make our recursive calls, the parent node passed in is the current node.

More to Explore

You have attempted of activities on this page