14.5. Priority queues¶

If we have a collection of elements that carry a “score”, then how can we find and remove the element with the smallest (or largest) score? What if new elements may be added at any time?

This collection is called a priority queue because:

Like std::queue, it is used to simulate objects waiting in line.
But instead of FIFO, the processing order is determined by the object “priority” or score.

Like std::stack and std::queue, std::priority_queue is an adapter that works on an underlying sequential container, which must provide random-access iterators (vector or deque). For example:

priority_queue<event, vector<event>> event_queue;

Priority queues are often used to manage scheduling. The classic example of a priority queue is an emergency room. Patients are not served in the order they arrive, but in order of severity.

In a software application, if we wanted to simulate urban traffic, we might create a series of events, some of which spawn other future events:

Simulated traffic light need an event for the next change. When a light changes to red, we schedule a change event to green some number of seconds later. When a light changes to green, we schedule a change-to-yellow event some time a little later, and so on.
Parking lots and garages might be simulated as objects that, at random time intervals, toss a new car out on to the street in front of the lot or garage. The car-generation interval might vary with the time of day (e.g., at 5:00PM, when everyone is leaving work, the interval between cars leaving each garage would be reduced).
Each moving car on the street would have an event associated with the time it needs to reach the next intersection along its path. When it reaches the intersection, we schedule a new event for the intersection after that, and so on.

while (simulation has not ended)
   get next event from event_queue
   trigger event
end while

In this example, the ‘priority’ value is time. Regardless of when an event is sent, we want the events to occur in their correct time order.

Although ‘queue` is in the name, a queue is not a good starting point for a priority queue implementation. However, there is a data type perfectly suited to this task – a heap. In fact, heaps are used to implement priority queues so often that the terms are often used interchangeably.

14.5.1. Heaps¶

A heap is a special tree-like data structure. There are many types of heaps, however, in this chapter, we will discuss only binary heaps. In this section, we will refer to binary heaps merely as heaps. A heap may be a binary tree, but it is not a binary search tree. Heaps have two key attributes:

The underlying tree must be complete
The order of elements must obey the heap property

For a min heap a parent element must be <= all its children.

For a max heap a parent element must be >= all its children.

One of the side-effects of heap is that the minimum (or maximum) value can always be found at the tree root.

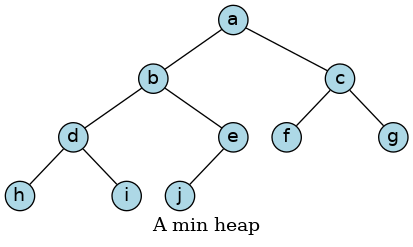
We can show that a complete binary tree of height \(h\) has between \(2h\) and \(2(h+1) − 1\) nodes. This implies that the height of a complete binary tree is \(\lfloor \log N \rfloor\), which results in \(O(\log N)\) performance.

Although logically a heap is a tree-like data structure, because the tree must be complete, it fits easily into an array or vector. It is very common to use an array for the physical implementation of a heap, since it is much more efficient than a general purpose tree bound together with pointers. For a tree of height \(2^h - 1\):

The parent of a node i is located at index \(\lfloor \frac{i}{2} \rfloor\)
The left child of a node i is located at index \(2i\)
The right child of a node i is located at index \(2i + 1\)

To get our math to work out nicely, we place the root node at index position 1. This storage location won’t go to waste – it is used when we remove nodes from the tree and maintaining the heap property is required.

The array representation of the min heap is:

Depending on the implementation, the backing store may or may not have extra storage.

The heap interface can be implemented as follows:

template <class T,
       class Container = std::vector<T>
       class Compare = std::greater<typename Container::value_type>>
   // require T is comparable
   class binary_heap
   {
     public:
       using value_type = T;
       using value_compare = Compare;
       static_assert((std::is_same<T, Container::value_type>::value),
         "heap type must match underlying container value type" );

       binary_heap() = default;

       // Construct a heap from an unsorted container
       explicit binary_heap(const Container& items);
       explicit binary_heap(std::initializer_list<T> list)

       constexpr void     clear() noexcept;
       constexpr bool     empty() const noexcept;
       constexpr bool      full() const noexcept;
       constexpr size_t    size() const noexcept;
       constexpr const T& front() const noexcept;

       void pop();
       void push (const T& value) noexcept;

     private:
       size_t size_ = 0;
       Container heap_ = {T{}};

       void percolate_down(size_t hole) noexcept;
       void build_heap() noexcept;
       void percolate_up(const T& value) noexcept;

   };

The defining operations of a heap are:

front

Peek at the heap root element.

pop

Remove a value while maintaining the heap property.

Calls percolate_down to perform the work.

Constructors

Creates a new underlying container of the container adaptor from a variety of data sources.

Calls build_heap to ensure the heap property satisfied when construction is complete.

push

Add a new value to the heap, while maintaining the heap property.

Calls percolate_up to perform the work.

In this implementation, any container that implements front(), push_back(), and pop_back() are candidates for the backing store. This example uses vector by default. The Compare class allows the same class to function as either a min heap (the default), or another comparison function. Using less would transform the heap into a max heap.

14.5.2. Percolate up¶

When a new node is added to the heap, we initially use push_back to append the new value to the ‘last’ open position in the tree (the hole). At this point the tree is still complete, but the new value is not in the correct position (except through some random stroke of luck). So after the initial push_back the heap property is violated and must be restored.

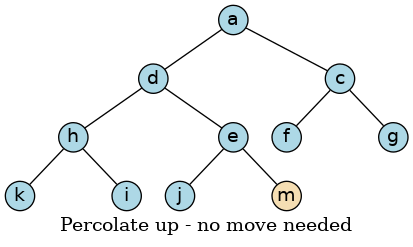
If however, the new value is less then its parent, it must be moved into a valid position.

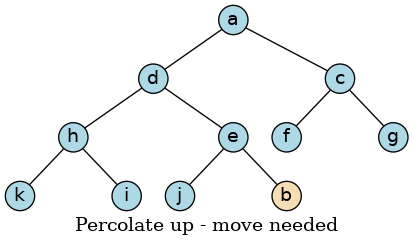
First we swap the value at position ‘b’ with the value at position ‘e’:

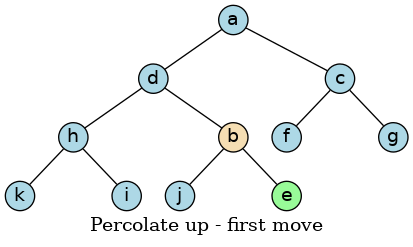
The value at position ‘d’ is still larger then ‘b’, so we are not done:

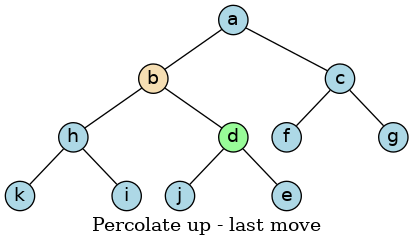
Now that ‘a’ is less than ‘b’ and all of the children of ‘b’ are greater than ‘b’, the heap property has been restored and we are done.

The percolate_up function does all the hard work. In truth, it is a fairly short function. The algorithm outline is:

percolate_up (value)
   heap[0] ← value
   hole ← last position in heap
   while (value < parent_of_hole)
      move parent value to hole
      set hole to parent position
   done while
   move heap[0] to heap[hole]
done percolate_up

The actual implementation is a lab exercise.

To implement push using percolate_up, we:

Increase backing store capacity, if needed.
Push the value onto the end of the tree.
Increase the tree size by 1.
Percolate up from the last node in the tree.

14.5.3. Percolate down¶

When we return a value from the top of the heap, we return the root node value. We now have a hole that needs to be filled. One approach is to move the last node in the heap to the root position and then ‘percolate_down’ to push the value to its proper location in the tree. This has a few of advantages;

It maintains the completeness property of our tree
It is relatively straightforward to implement. The same algorithm can be used independent of the tree structure or any node value.

Since this is a little more complicated than percolate_up, the entire function is shown. The main complication is that the current node might have 0 children, 1 child, or 2 children, so we need to be careful that we don’t try to access the value of non-existent children.

void percolate_down(size_t hole) noexcept
{
  T tmp = std::move(heap_[hole]);

  for (size_t child; hole*2 <= size_; hole = child) {
    child = hole*2;
    if (child != size_ && heap_[child+1] < heap_[child]) {
      ++child;
    }
    if (heap_[child] < tmp) {
      heap_[hole] = std::move(heap_[child]);
    } else {
      break;
    }
  }
  heap_[hole] = std::move(tmp);
}

A walk-through follows. When we pop ‘a’ from the heap, we leave a space that must be filled while maintaining the heap property.

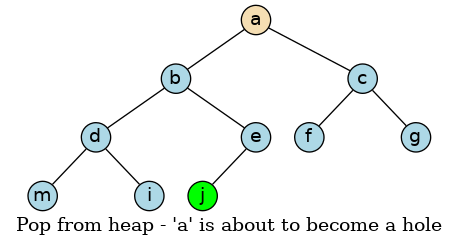
Grab the last value in the tree, which may or may not be the largest value. Move this value into the root position. Since the largest value is in the root position, the heap property is no longer valid. We have to restore the heap property by pushing this value down until the heap property is restored.

We can achieve this by continually exchanging the smallest child value with the current value until the heap property is restored.

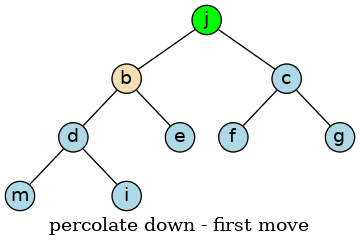
The ‘j’ is still larger than ‘d’, so again, we exchange the two values.

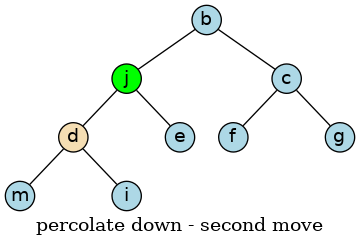
When we check the left node, the value ‘j’ is less then ‘m’. We can’t stop at this point, because this node has another child. The ‘j’ is still larger than ‘i’, so we exchange values, however this time we traverse the right sub tree.

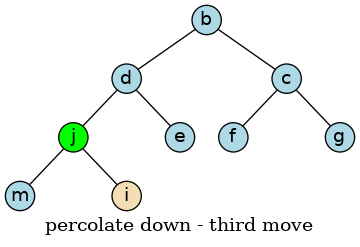
At this point, the node ‘j’ has no children, so we are done.

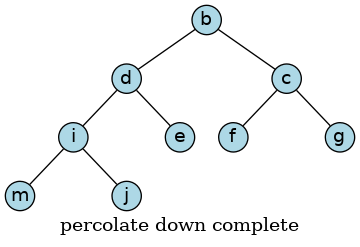
To implement pop using percolate_down, we:

Move the last tree node to the root.
Reduce the tree size by 1
Percolate down from the root node.

Build heap

Frequently we want to create a binary heap from an existing collection which could be the template type Container or an initializer_list<T> in our example heap. These constructors take \(N\) arbitrarily items and transforms them into a heap. We could achieve this with \(N\) successive inserts. Each insert will take \(O(1)\) average and \(O(log N)\) worst-case time, the total running time of this algorithm would be \(O(N)\) average but \(O(N log N)\) worst-case. Since this is a special instruction and there are no other operations intervening, and we already know that the instruction can be performed in linear average time, it is reasonable to expect that with reasonable care a linear time bound can be guaranteed.

The general algorithm is to place all the items into the tree in any order, maintaining the structure property. Then, if percolate_down(i) percolates down from node i, the buildHeap routine in Figure 6.14 can be used by the constructor to create a heap-ordered tree.

To implement build_heap using percolate_down, we:

Copy all items from the source container or range into the heap backing store in any order. As long no uninitialized values are present in the range \(\left [ begin(), end() \right )\), then the heap structure is maintained and only the heap order property needs work.
Call percolate_down starting from the heap midpoint and iterate down to the root node.

The actual implementation of build_heap is a lab assignment.

More to Explore

The content on this page was adapted from Binary Search Trees, by Steven J. Zeil for his data structures course CS361.
std::priority_queue
Heap data structures

You have attempted of activities on this page