15.7. Analysis of hash tables¶

The table below shows the average case Big-O efficiency of some basic unordered_map operations. For each operation that has average case constant time efficiency, the worst case complexity is \(O(n)\).

**Big-O Efficiency of C++ unordered map Operators**¶
Operation	Big-O Efficiency
assignment =	O(1)
insert()	O(1)
find()	O(1)
contains()	O(1)
erase()	O(1)
clear()	O(n)

The reason these operations may have \(O(n)\) complexity is because the performance of the container is ultimately controlled by the quality of the hash function for the key type in the container. If the hash function performs poorly (many collisions), then the benefits of hash tables are lost and we decay into list performance. When the hash function quality is high, then the performance is good.

When we discussed the messy and neat closets in Tree ADT concepts, we mentioned the primary motivation for non-sequential containers was search. Unlike even a sorted vector or a tree, hash tables provide constant time access tot he correct bucket containing our data and linear search is required only when collisions exist.

The following code shows what happens when searching in an unordered map vs a vector.

#include <algorithm>
#include <chrono>
#include <iomanip>
#include <iostream>
#include <numeric>
#include <unordered_map>
#include <vector>

int main() {
    using clock = std::chrono::high_resolution_clock;
    std::cout << std::setw(6) << "size"
              << std::setw(10) << "vector"
              << std::setw(20) << "hash table\n";
    // for(int size = 10'000; size < 100'001; size += 20'000) {
    int size = 35000;
        // fill vector
        std::vector<int> sequence (size);
        std::iota(sequence.begin(), sequence.end(), 0);
        // search vector
        auto begin = clock::now();
        for(const auto& it: sequence){
            if(std::find(sequence.begin(), sequence.end(), it) == sequence.end()) {
                std::cerr << "Failed to find an expected value in vector! Halting.\n";
                return -2;
            }
        }
        auto end = clock::now();
        std::chrono::duration<double> elapsed_secs = end - begin;
        // fill hash table
        std::unordered_map<int, int> table;
        for(int item = 0; item < size; ++item){
            table[item] = item;
        }
        begin = clock::now();
        // search hash table
        for(const auto& it: table){
            if(table.find(it.first) == table.end()) {
                std::cerr << "Failed to find an expected value in map! Halting.\n";
                return -2;
            }
        }
        end = clock::now();
        std::chrono::duration<double> elapsed_secs_ht = end - begin;

// Printing final output
        std::cout << std::fixed   << std::setprecision(4)
                  << std::setw(6) << size << '\t'
                  << std::setw(8) << elapsed_secs.count() << '\t'
                  << std::setw(8) << elapsed_secs_ht.count() << '\n';
    // }
    return 0;
}

Try This!

The online compiler is limited in both memory and time allowed.

Run this example on your own computer with the loop enabled and with larger values and compare.

The vector is linear in std::distance(begin, end) and as expected, the hash table is constant time. Running the previous code should produce results similar to this:

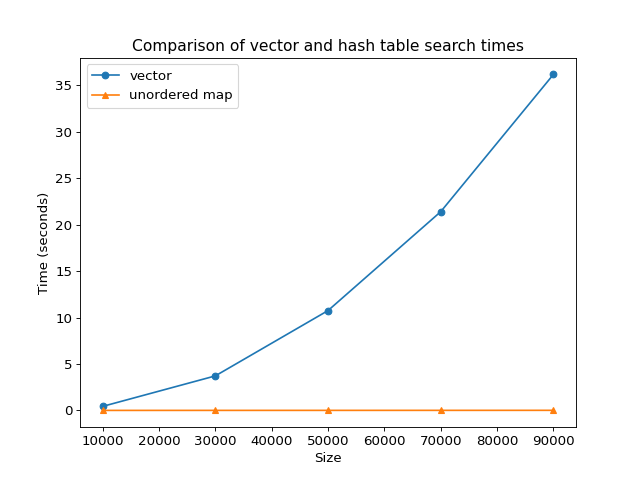
Comparison of vector and hash table search times

So what about the tree ADT? The std::set is generally implemented as a tree. The C++ standard guarantees logarithmic complexity in the size of the container.

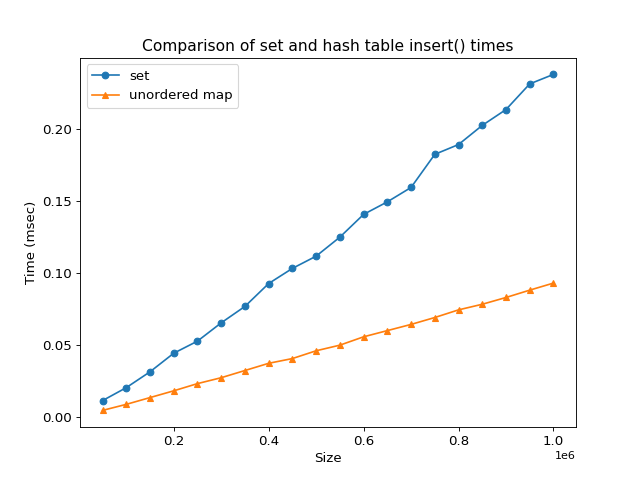
How does std::set find compare to std::unordered_map find?

#include <algorithm>
#include <chrono>
#include <iomanip>
#include <iostream>
#include <numeric>
#include <set>
#include <unordered_map>

int main() {
    using clock = std::chrono::high_resolution_clock;
    std::cout << std::setw(6) << "size"
              << std::setw(10) << "set"
              << std::setw(20) << "hash table\n";
    for(int size = 5'000; size < 100'001; size += 5'000) {
        // fill set
        std::set<int> tree;
        for(int item = 0; item < size; ++item){
            tree.insert(item);
        }
        // search set
        auto begin = clock::now();
        for(const auto& it: tree){
            if(tree.find(it) == tree.end()) {
                std::cerr << "Failed to find an expected value in set! Halting.\n";
                return -2;
            }
        }
        auto end = clock::now();
        std::chrono::duration<double> elapsed_secs = end - begin;
        // fill hash table
        std::unordered_map<int, int> table;
        for(int item = 0; item < size; ++item){
            table[item] = item;
        }
        begin = clock::now();
        // search hash table
        for(const auto& it: table){
            if(table.find(it.first) == table.end()) {
                std::cerr << "Failed to find an expected value in map! Halting.\n";
                return -2;
            }
        }
        end = clock::now();
        std::chrono::duration<double> elapsed_secs_ht = end - begin;

Although the std::set find is logarithmic complexity, from a practical sense, it compares favorably with the hash table. The graph below shows example output for values up to 1,000,000.

Comparison of set and hash table find times

Try This!

The online compiler is limited in both memory and time allowed.

Run this example on your own computer with larger values and compare.

More to Explore

You have attempted of activities on this page